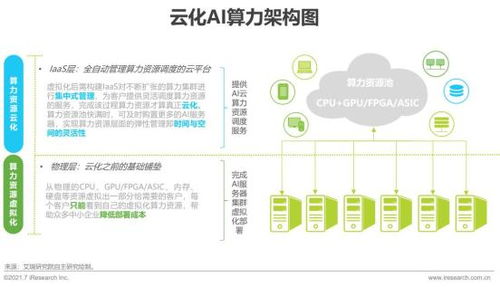
人工智能基础与线性回归模型在软件开发中的核心应用
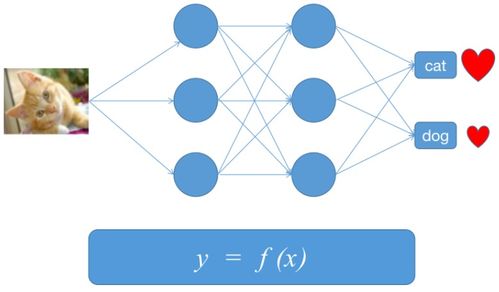
人工智能(AI)作为当今科技领域的前沿技术,正深刻改变着软件开发的方式与效率。其中,线性回归模型作为机器学习中最基础且广泛应用的算法之一,为AI软件开发提供了坚实的理论基础与实践工具。
在人工智能基础中,线性回归模型通过建立自变量与因变量之间的线性关系,实现对数据的预测与分析。其数学表达式为 y = β₀ + β₁x₁ + ... + βₙxₙ + ε,其中y代表预测值,x为特征变量,β为模型参数,ε为误差项。这一简洁而强大的模型形式,使其成为众多复杂AI系统的构建基石。
在软件开发实践中,线性回归模型的应用主要体现在以下几个方面:
在数据预处理阶段,开发者可利用线性回归进行特征重要性分析,识别对目标变量影响最大的因素,从而优化特征工程过程。例如在电商推荐系统开发中,通过分析用户行为特征与购买意愿的线性关系,可有效提升推荐准确率。
在模型原型开发阶段,线性回归常作为基准模型,为后续更复杂的神经网络或集成学习模型提供性能对比参考。其训练效率高、解释性强的特点,使其特别适合在项目初期进行快速验证和迭代。
在工业级AI系统开发中,线性回归模型因其稳定性和可解释性,常被用于风险评估、销量预测等关键业务场景。结合现代软件开发框架如TensorFlow、PyTorch或Scikit-learn,开发者能够快速实现模型的部署与集成。
值得注意的是,虽然线性回归模型相对简单,但在实际软件开发中仍需考虑多重共线性、异方差性等问题。开发者需要通过正则化、特征标准化等技术手段优化模型性能,同时结合交叉验证等方法确保模型的泛化能力。
随着AI技术的不断发展,线性回归模型也在持续演进。多项式回归、岭回归等变体形式的出现,进一步拓展了其应用范围。在当今的AI基础软件开发中,理解并熟练运用线性回归模型,已成为开发者必备的核心技能之一。
线性回归模型作为人工智能领域的基础算法,不仅为复杂AI系统开发提供了重要支撑,更通过其简洁性和可解释性,帮助开发者构建更加可靠、高效的软件解决方案。在未来的AI软件开发浪潮中,这一经典模型仍将发挥不可替代的作用。
如若转载,请注明出处:http://www.1024planet.com/product/36.html
更新时间:2025-11-29 02:32:35